实测 DeepSeek R1 Lite 预览版，看看它是否比 GPT o1 更好

DeepSeek 刚刚推出了DeepSeek-R1-Lite-Preview模型，有人声称它甚至比 OpenAI 的o1-preview模型还要好。这是否只是 AI 炒作的又一波浪潮？

我在网上看到过关于该模型卓越推理能力和透明决策的大胆言论。据说它在复杂任务（尤其是数学和编码）中表现出色，据报道在 AIME 和 MATH12 等严格基准测试中匹敌甚至超越了 OpenAI 的 o1 预览版。

我很好奇，所以我决定亲自在编码挑战、高级数学问题和自然语言处理上测试这些说法。让我们看看 DeepSeek-R1-Lite-Preview 到底有多好。

deepseek-r1-lite-preview?-什么是 DeepSeek-R1-Lite-Preview？

DeepSeek-R1-Lite-Preview 是一款类似于ChatGPT的 AI 工具，由中国公司 DeepSeek 创建。该公司于 11 月 20 日在X上宣布了这一新模型（推文链接），并在文档页面上分享了一些细节。

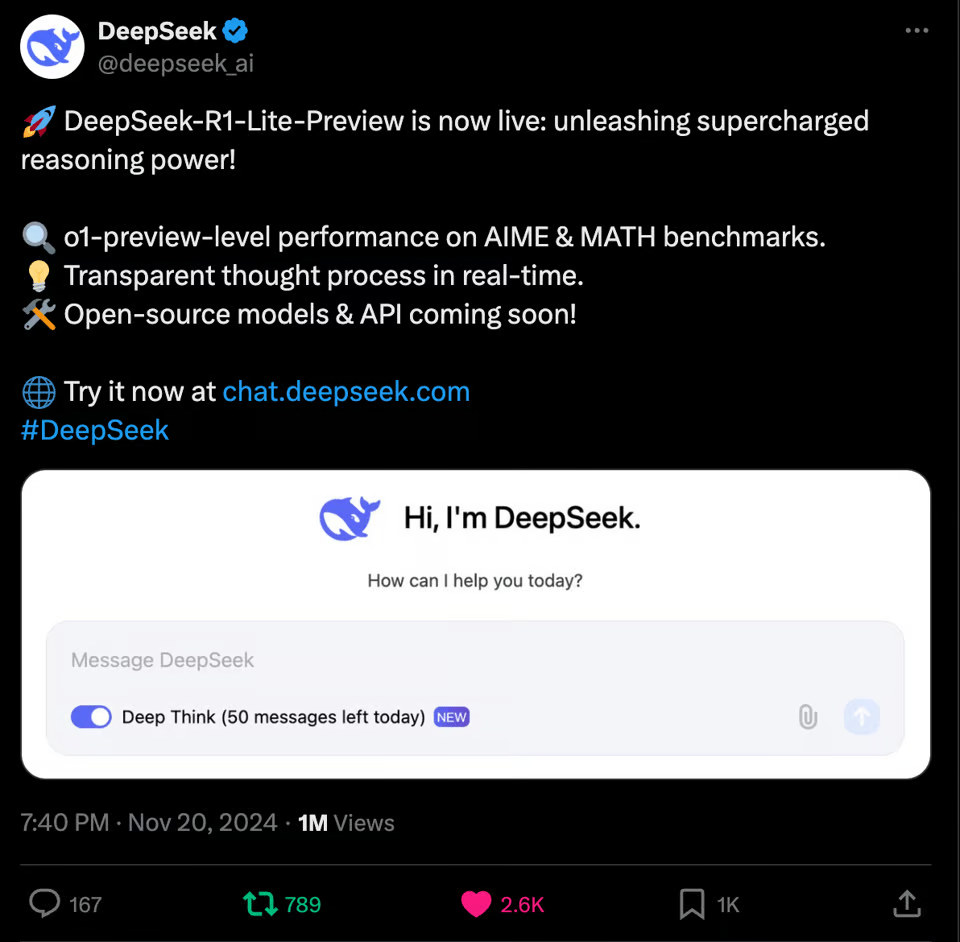
DeepSeek-R1-Lite-Preview 旨在真正擅长解决数学、编码和逻辑方面的复杂推理问题。它会逐步向您展示它的思考方式，以便您了解它如何得出答案，这有助于人们更加信任它。

您可以免费在其网站chat.deepseek.com上试用，但在其高级模式“深度思考”中，您每天只能发送 50 条消息。DeepSeek 还计划向公众分享该工具的部分功能，以便其他人可以使用或在此基础上进行开发。

如何使用 DeepSeek-R1-Lite-Preview

您可以按照以下两个步骤开始使用 DeepSeek-R1-Lite-Preview：

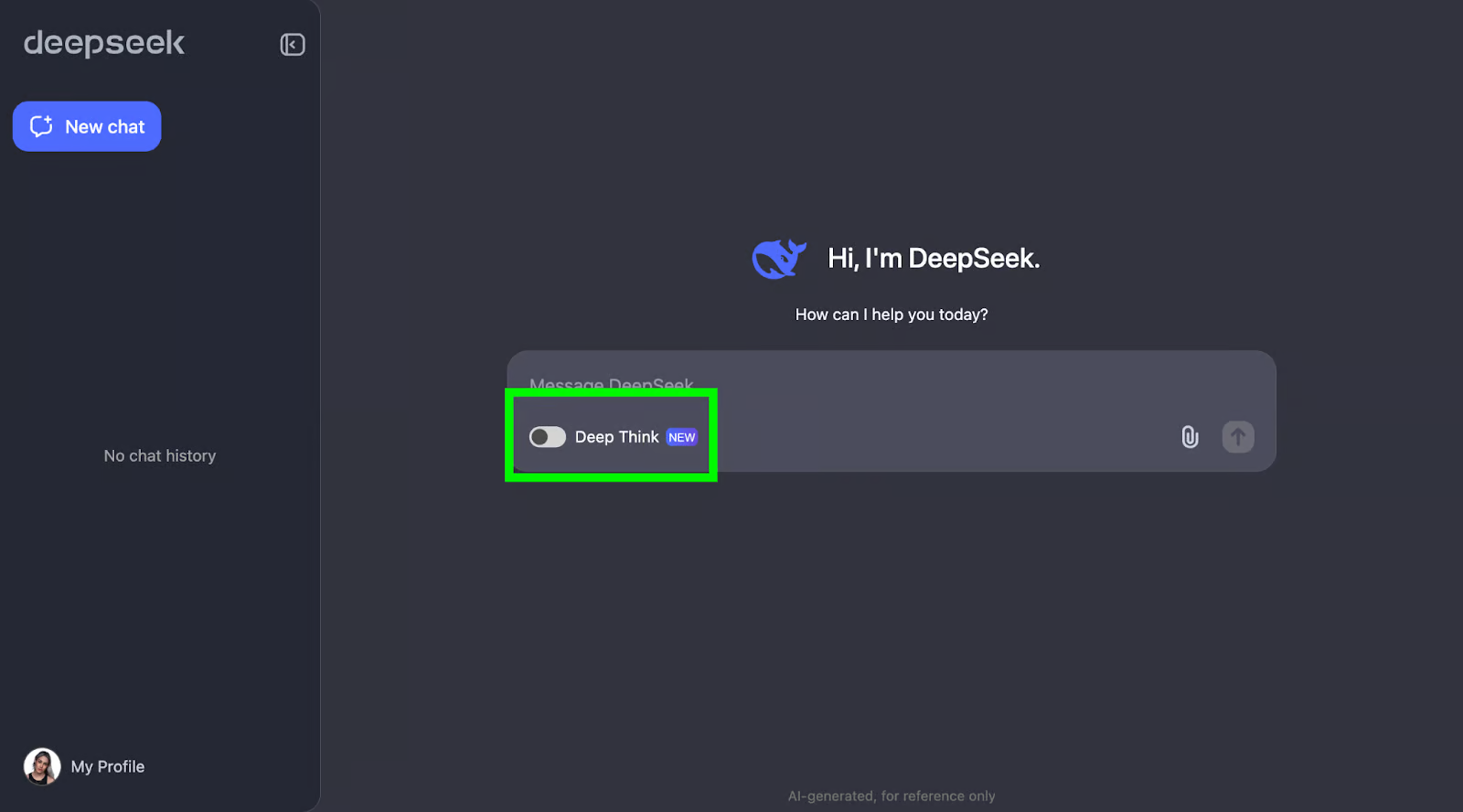
1. 访问DeepSeek 聊天页面并登录。
2. 启用“深度思考”。

草莓测试

要了解 DeepSeek-R1-Lite-Preview 的功能，让我们来测试一下！我将进行一系列挑战，展示其推理能力，首先是简单但著名的草莓问题：字母“r”在“strawberry”中出现了多少次？

这个问题看起来很简单，但 LLM（甚至GPT-4o）历来都很难正确回答它——他们通常回答字母“r”只出现了两次。

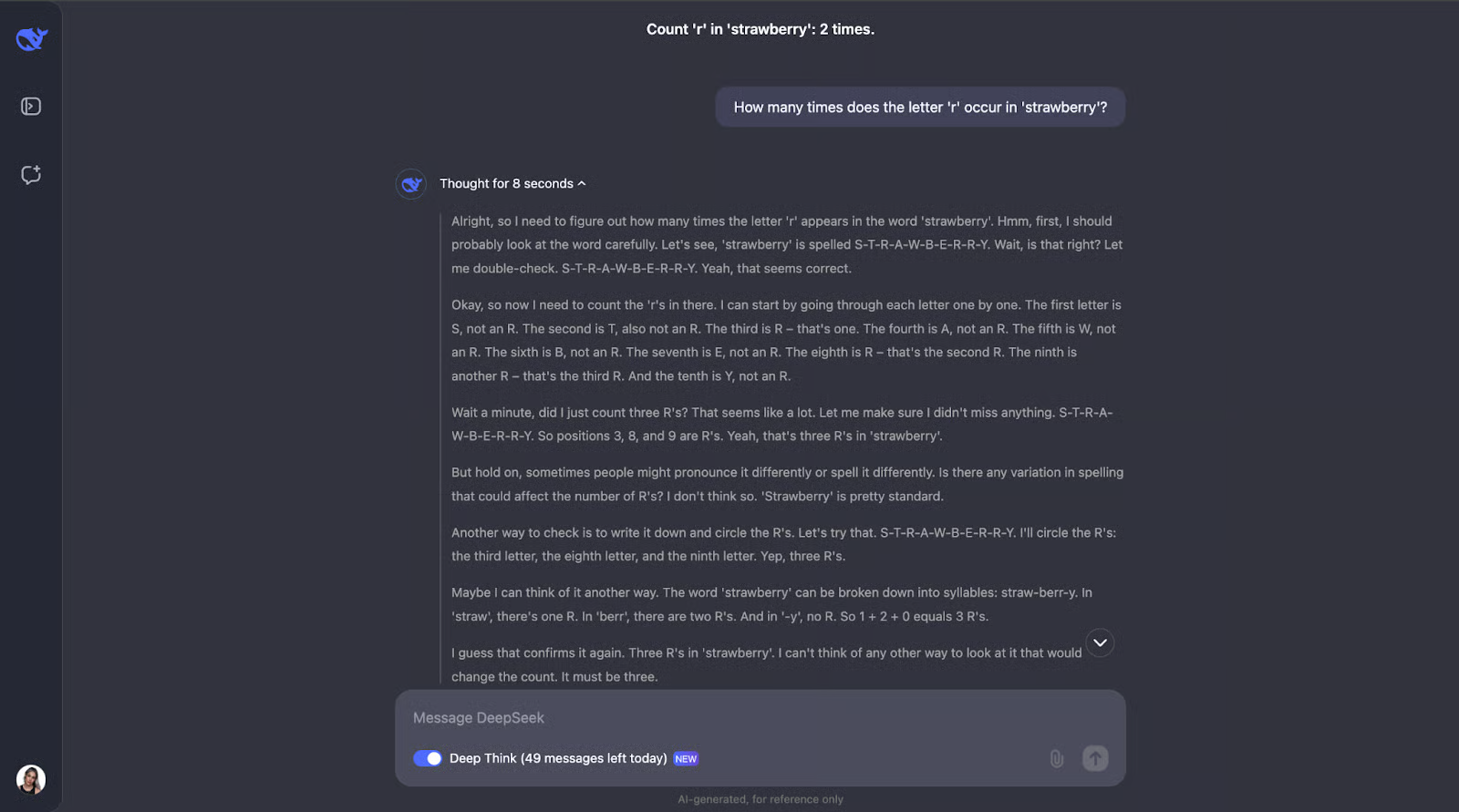
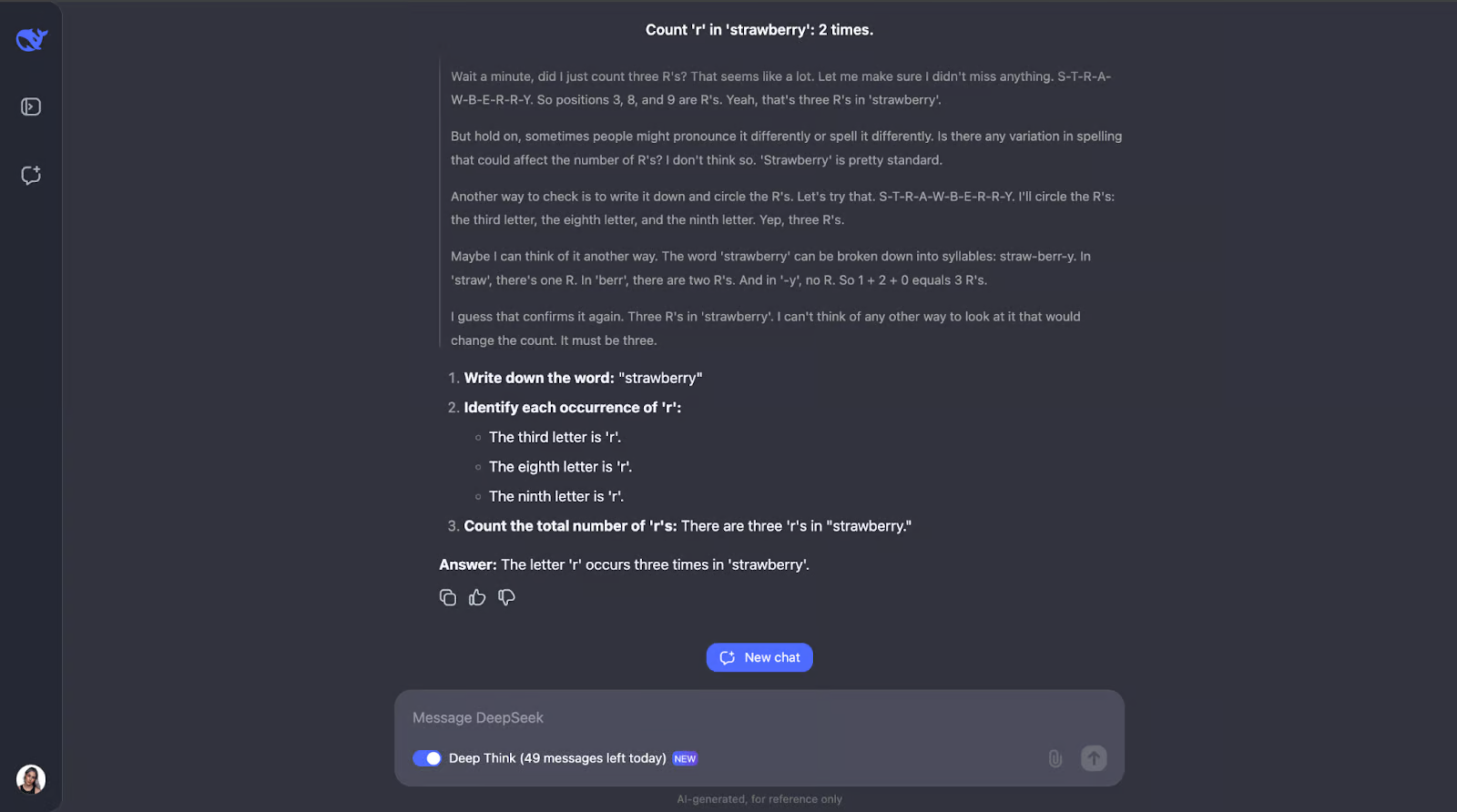
哇，好吧——我没想到这个看似简单的任务竟然需要这么长的推理过程。我以为在数完字母“r”并确定它在单词中的位置后，它就会停在那里。但令我感兴趣的是，它并没有就此止步。它反复检查了几次计数，甚至考虑了人们可能会如何发音或拼写这个单词等问题——我认为这有点多余，尤其是发音部分。但这确实表明它是多么细心和周到！它还解释了每一步，这样我就可以跟上它的思维过程，看看它是如何得出答案的。

数学推理

我将通过三个数学问题测试 DeepSeek-R1-Lite-Preview。

三角面积

鉴于 DeepSeek 声称自己非常擅长数学推理，让我们从一个简单的几何问题开始吧。

“如果一个三角形的边长为 3、4 和 5，那么它的面积是多少？”

这个问题需要毕达哥拉斯定理和海伦公式的知识。我希望 DeepSeek-R1-Lite-Preview 能够展示其工作，可能像这样：

• 识别出这是 3-4-5 直角三角形
• 计算半周长：s = (3 + 4 + 5) / 2 = 6
• 应用海伦公式：面积 = √(s(sa)(sb)(sc))
• 替换值：面积 = √(6(6-3)(6-4)(6-5)) = √(6 * 3 * 2 * 1) = √36 = 6
• 验证：直角三角形面积 = (底边 * 高) / 2 = (3 * 4) / 2 = 6

让我们看看会发生什么！

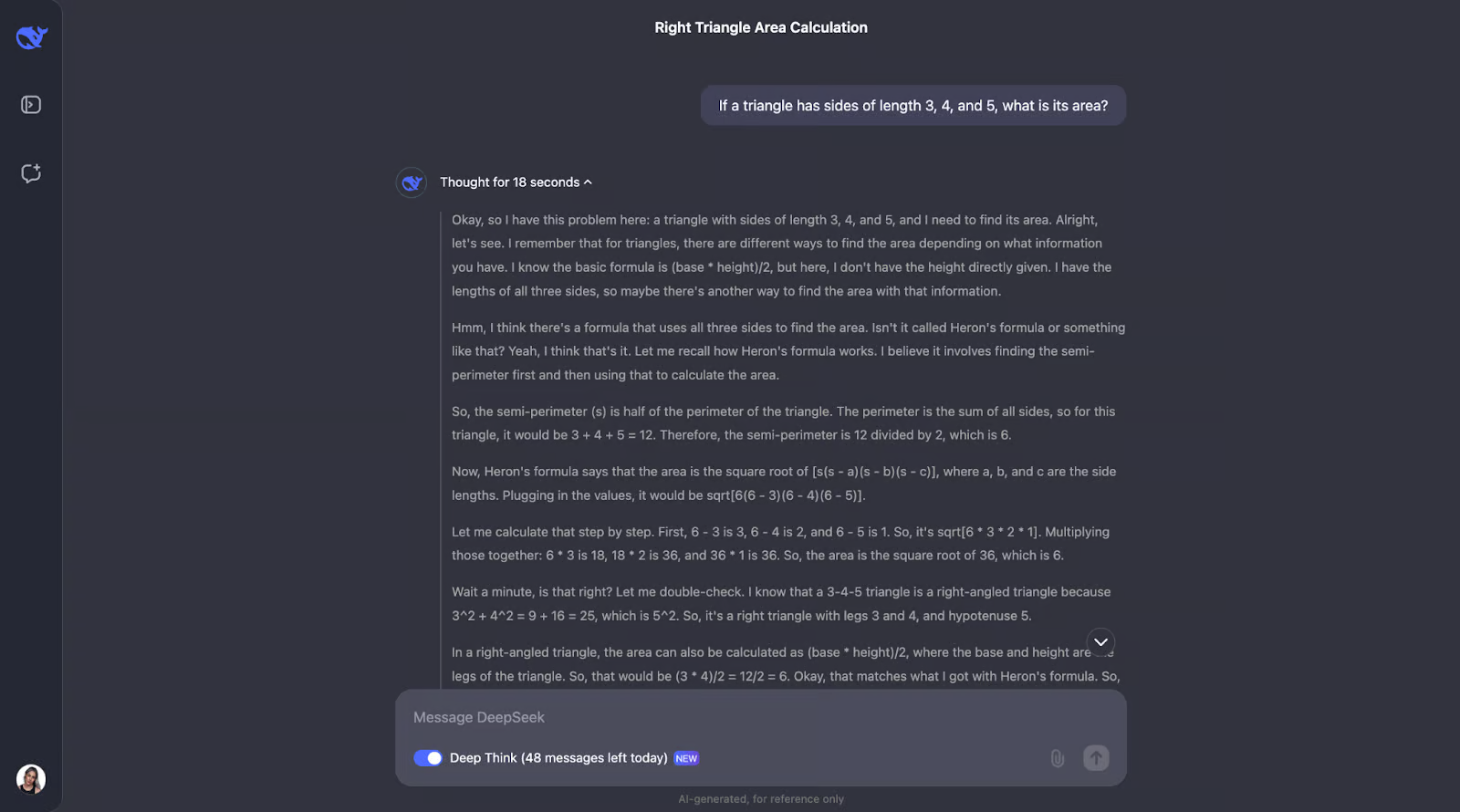
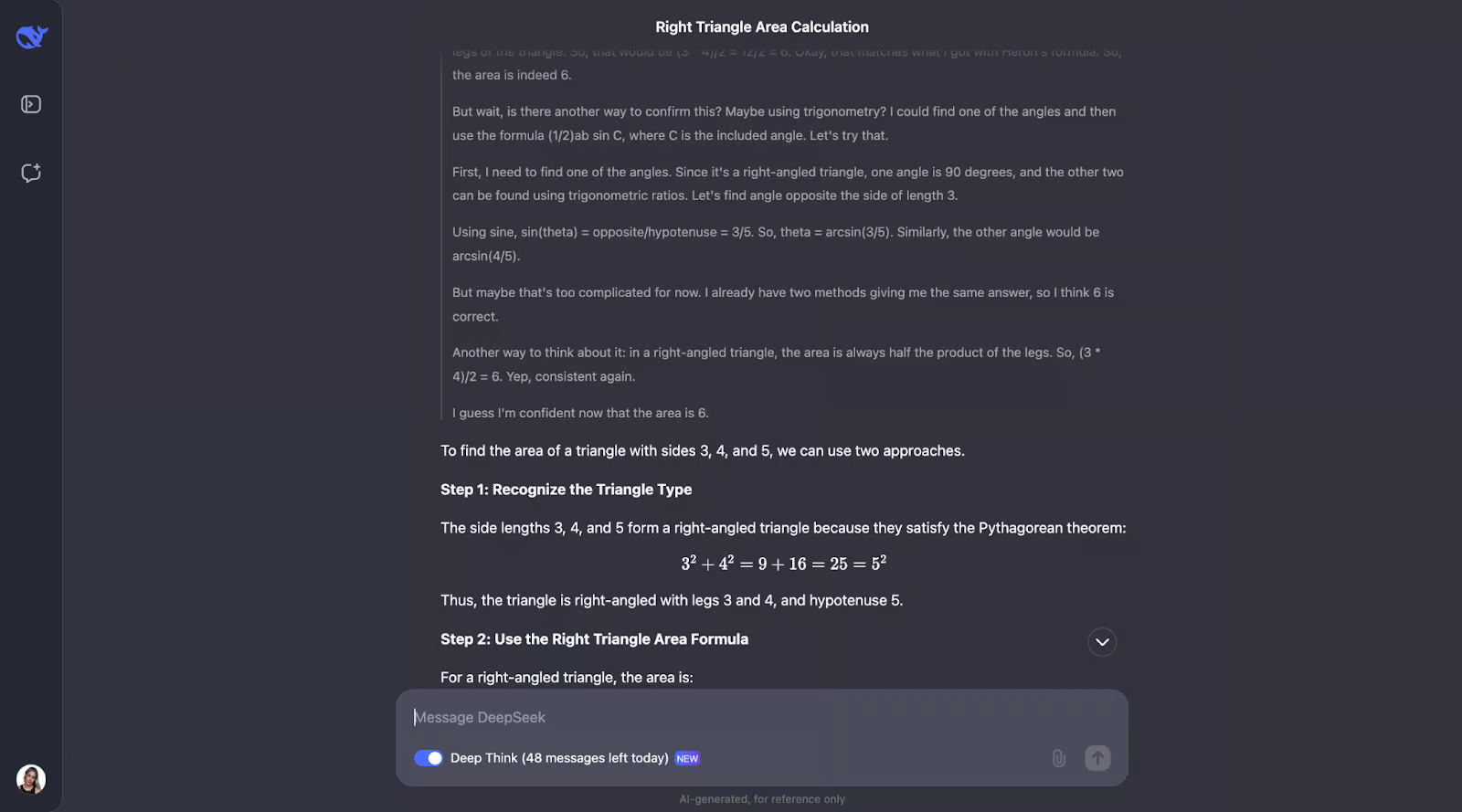
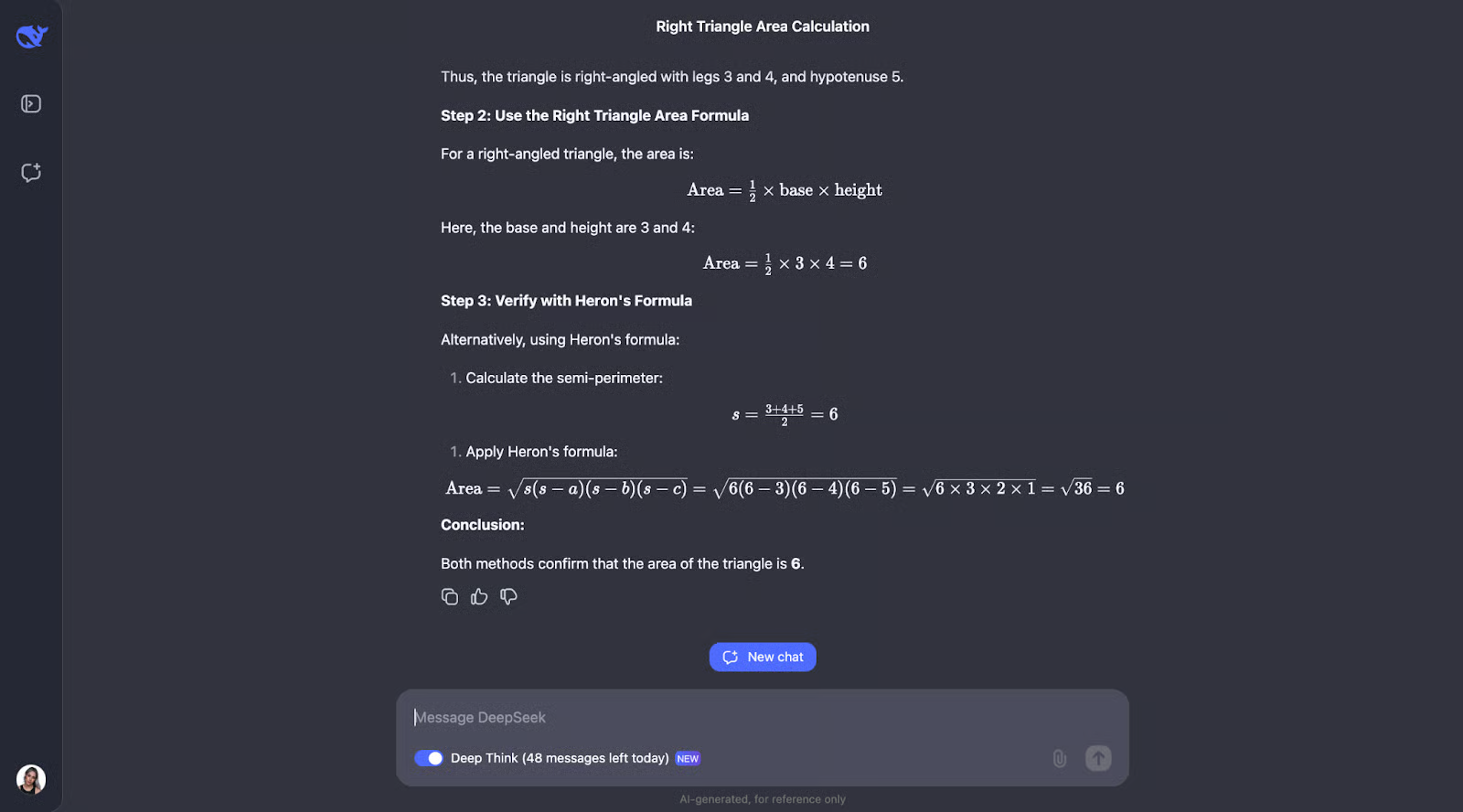
好吧，有趣的是，它执行了我预测的检查——尽管顺序不同。它还考虑使用三角函数计算角度并尝试另一个公式。我觉得这很有趣，最后它决定不需要这样做，因为前两种方法已经确认了答案。

解释和输出都特别清晰易懂，这让我觉得这将是一个很棒的模型，可以嵌入到数学学生的助手中。对于这个特定的用例，也许可以先展示思维过程，然后学生可以与之互动，在继续得出最终答案之前确认他们是否理解了它。

数学证明

让我们进行更复杂的数学测试，看看表现和思维过程是否存在差异。

“证明斐波那契数列的倒数之和收敛于一个有限值。”

这个测试考验模型对高级数学概念的理解，比如级数收敛和斐波那契数的性质。让我们来试试吧！为了便于阅读，我只会发布答案的第一部分和最后一部分（但您可以随意用相同的提示自己尝试一下）：

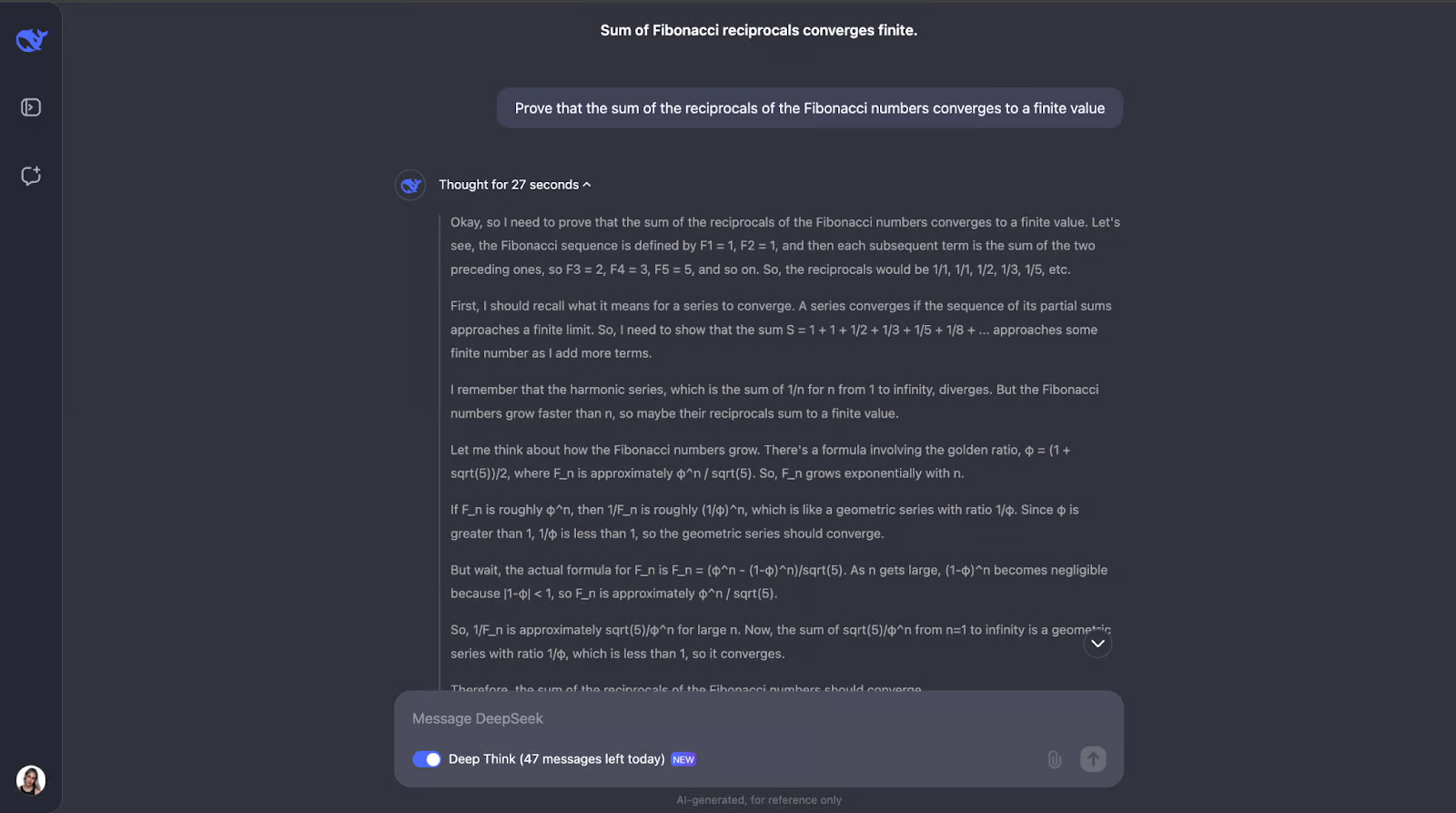
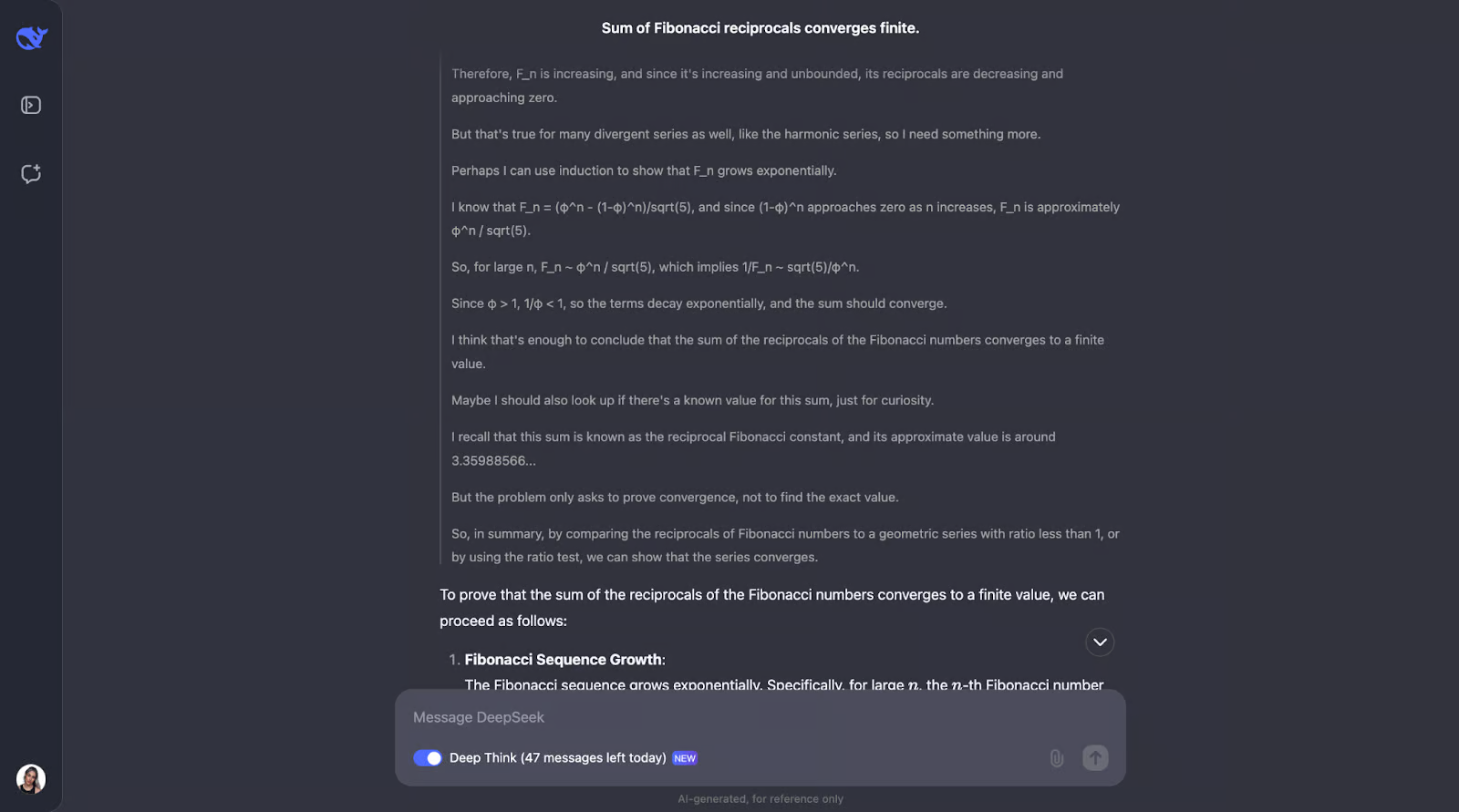
好的，这是一个很棒的思路——我真的很喜欢它首先确保理解关键概念，例如倒数和收敛。然后，DeepSeek-R1-Lite-Preview 通过查看斐波那契数的增长方式并使用比较测试来解决这个问题，这是测试序列是否收敛的常用方法。

它将斐波那契数列的倒数与几何级数进行比较。由于斐波那契数列的倒数比公比小于 1 的几何级数下降得更快，因此该模型得出结论，倒数之和也会收敛到一个有限值。为了更加确定，它使用了一种称为比率测试的方法。

此测试检查连续项比率的极限是否小于 1。如果是，则该级数收敛。该模型计算了斐波那契数的倒数的比率，发现它确实小于 1。

它甚至提到，这个和有一个已知值，称为斐波那契常数的倒数，约为 3.3598。但对于这个问题，我们只需要知道和是有限的，而不是确切的和是多少——所以这是我觉得很有趣的额外信息。我真的很喜欢解决方案在输出中的呈现方式。它很清晰，循序渐进。 

到目前为止，数学任务给我留下了深刻的印象。

微分几何

我要尝试一道微分几何问题——因为我的博士学位是这个领域的，所以我忍不住做了一个小测试。没有什么太复杂的，只是你在本科数学课上可能会遇到的一个经典练习。

“考虑 R³ 中的曲面 S，其参数为

φ(u,v) = (u cos v, u sin v, ln u)

其中 u > 0 且 0 ≤ v < 2π。

a) 计算S的第一基本形式。

b) 判断 S 是否为极小曲面。

c） 求出 S 的高斯曲率 K 和平均曲率 H。”

我希望 DeepSeek-R1-Lite-Preview 能够提供分步解决方案，展示所有计算并解释每个结果的意义以及主要概念的定义，例如基本形式、最小曲面和不同曲率。

为了让这个博客保持可读性，我只能显示答案的第一部分和最后一部分，但我鼓励你自己尝试一下：

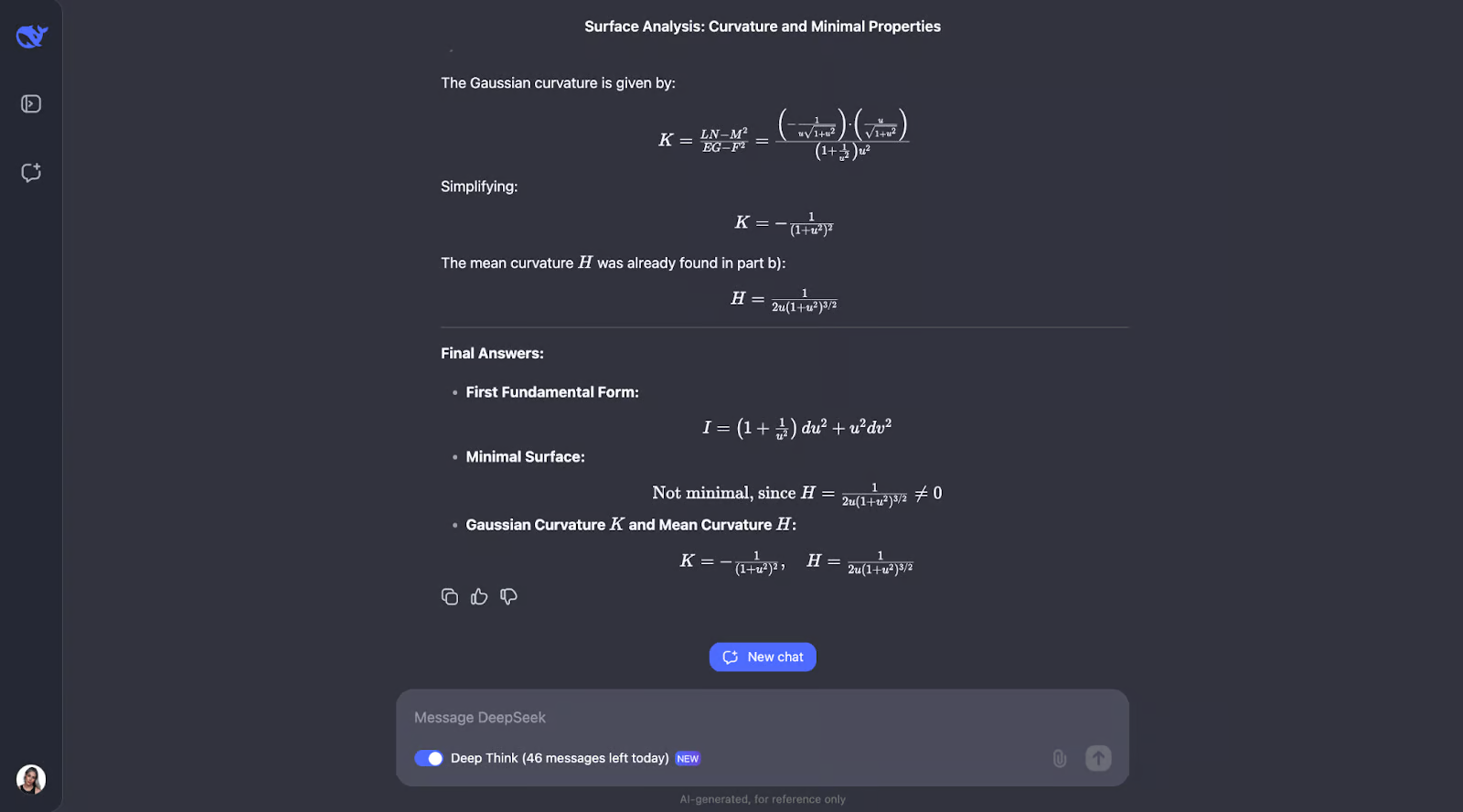
循序渐进的方法使用众所周知的几何公式​​并直接应用它们，这使得推理变得容易理解。然而，我本以为它会检查自己对问题中主要概念的理解，这不是思路的一部分。对于 B 部分，它采用了另一种方法，并确定所涉及的表面是旋转表面，这是一个很好的点子。

还有一次，它评论旋转并意识到它已经有了法向量 N，这可能与第二基本形式的系数符号相冲突。我希望看到关于更好符号的建议，因为对两件事使用同一个字母并不是好的做法！ 

当计算平均曲率时，它注意到它不为零，并质疑计算是否正确。为了彻底检查，它尝试了另一种方法来仔细检查其工作。

再次，输出非常清晰且易于理解。在所有这些示例中，令人印象深刻的是它如何始终使用不同的方法复查计算。思维过程始终详细、合乎逻辑且易于理解！

编码测试

现在让我们进入编码测试。

Python

我要测试的第一个是：

“用 Python 实现一个函数，找出给定字符串中最长的回文子串。该函数的时间复杂度应优于 O(n^3) 。”

我正在尝试评估该模型设计高效算法并在代码中实现它们的能力。我希望得到一个使用动态规划或 Manacher 算法的解决方案，并清晰地解释该方法和时间复杂度分析。

输出非常非常长，我只显示第一部分和最后一部分：

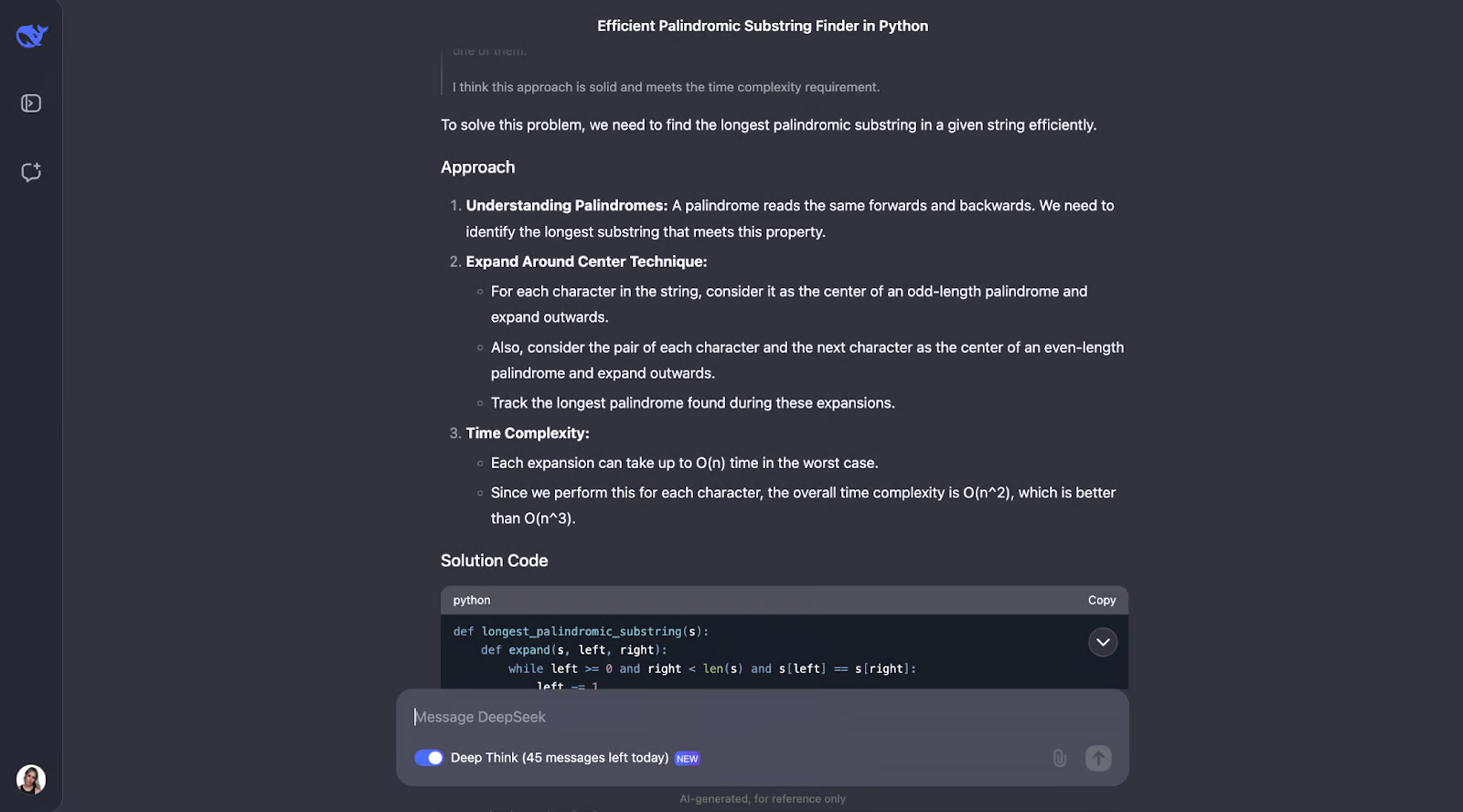
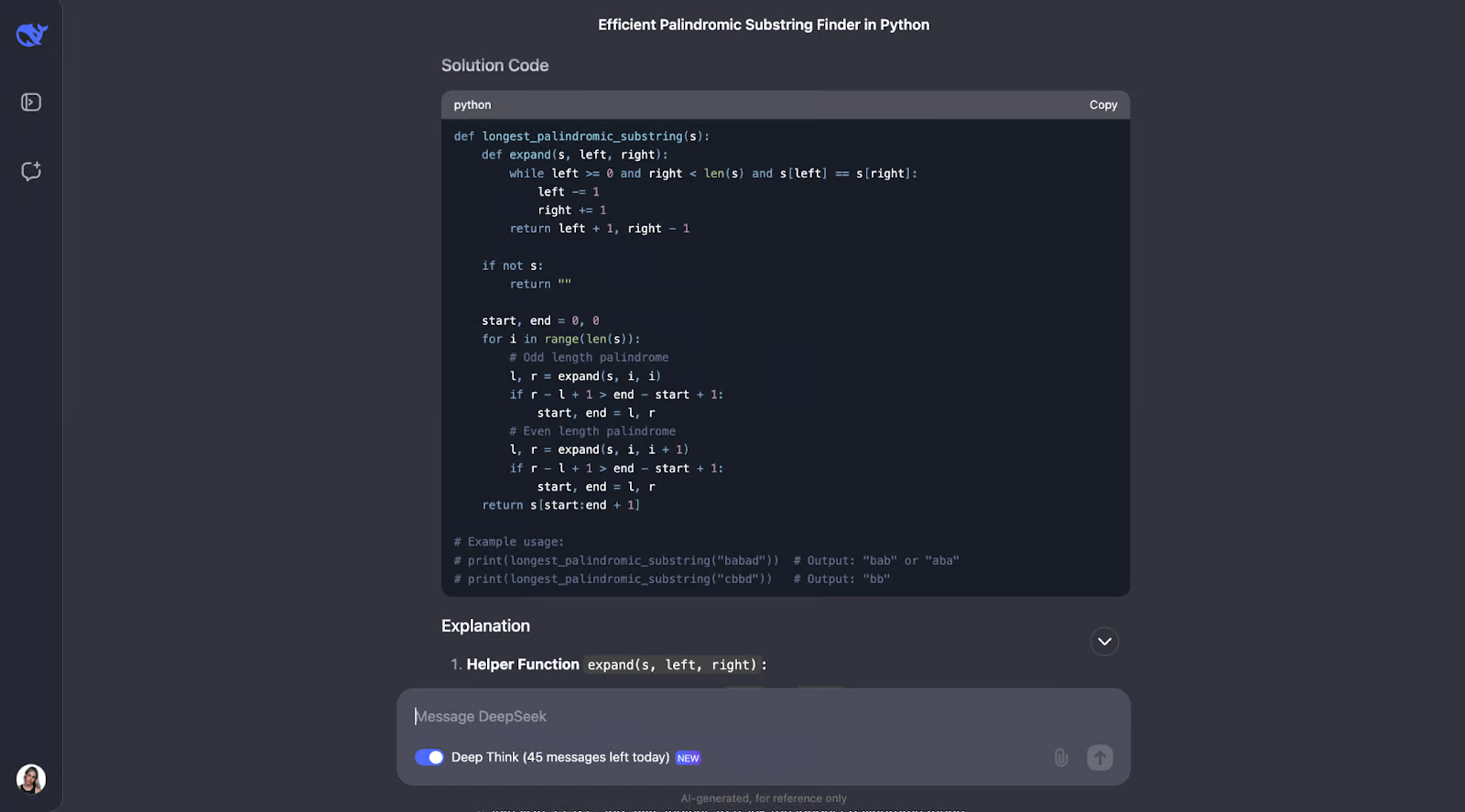
我认为该模型在解决寻找最长回文子串的问题上做得很好。它的方法很聪明、高效，而且解释得很清楚。

它没有使用强力方法强制执行所有可能的子字符串（这会很慢），而是使用了一种巧妙的“围绕中心扩展”技术。这种方法既能处理奇数长度的回文，如“aba”，也能处理偶数长度的回文，如“abba”。它会在执行过程中跟踪找到的最长回文。结果是一种运行时间为 O(n^2) 的算法，比 O(n^3) 的解决方案快得多。 

这个答案给我留下的最深刻印象是它呈现得非常清晰。DeepSeek 将问题分解为易于理解的步骤，详细解释了其思维过程，甚至还提供了实际示例。例如，它展示了算法如何围绕“racecar”或“abba”的中心展开以找到正确的回文。在我看来，围绕中心展开的辅助函数特别好 – 它使代码模块化且易于理解。

话虽如此，我原本希望它能考虑 Manacher 算法，这是一种更快的 O(n) 解决方案。它的实现肯定更复杂，但它在性能至关重要的情况下很有用，我原本希望模型能指出这一点。 

我还注意到输出没有明确讨论算法如何处理特殊情况，例如空字符串或所有字符都相同的字符串（例如“aaaa”）。这些情况是可行的——但我希望它至少会讨论这一点。 

最后，我认为它对示例用法的预期输出进行了注释，这一点很好。但是，当我运行代码时，只打印了第一个示例用法的第一个选项。如果代码考虑了所有可能的解决方案并将它们全部打印出来，那就太好了。

JavaScript

让我们用另一种编程语言尝试不同的编码问题。

“用 JavaScript 编写一个函数来确定给定的数字是否为素数”

为了便于阅读，我仅显示第一部分和最后一部分（尽管这次思路链要短一些）：

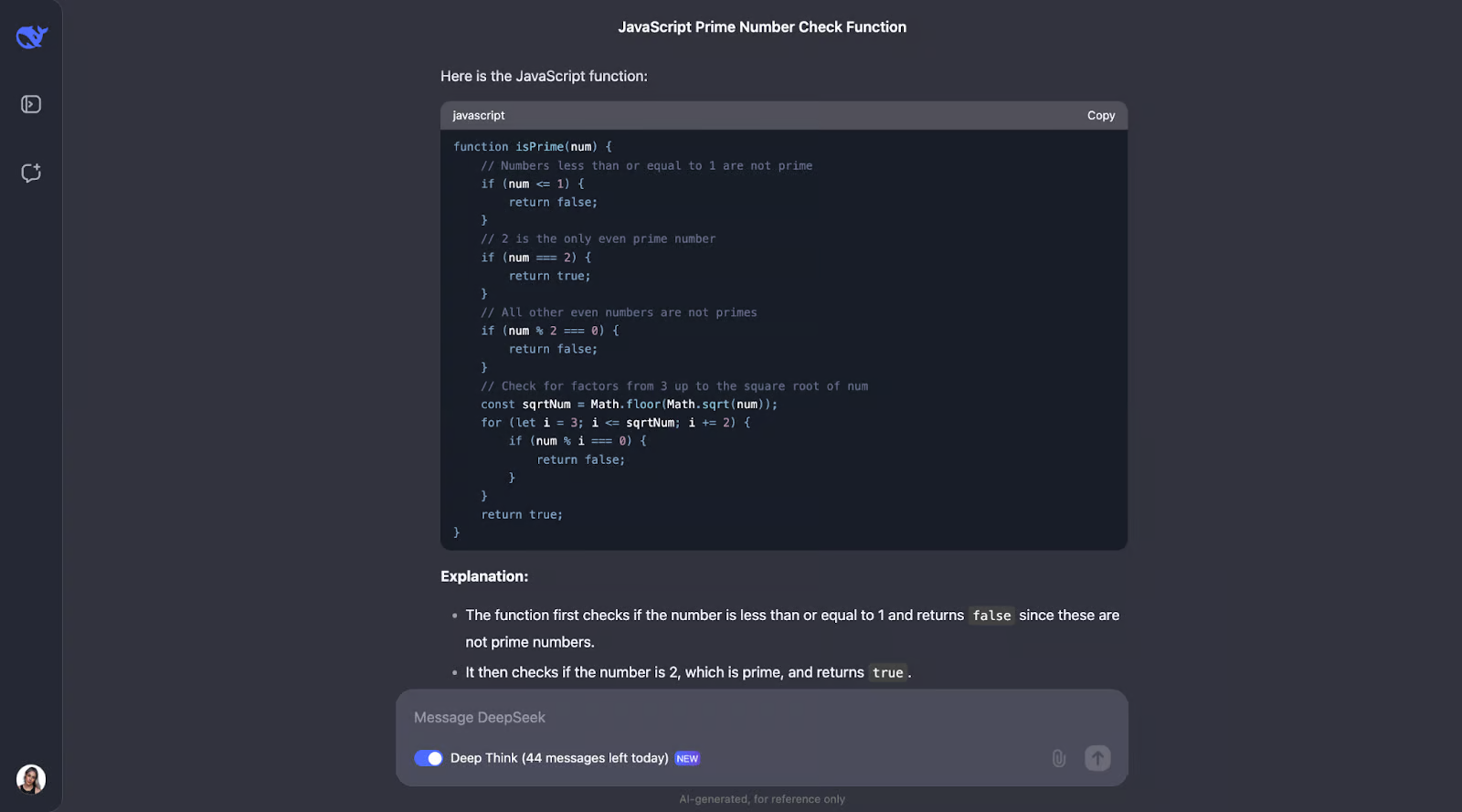
我认为我们可以从这里看出思维过程的规律。大多数情况下，它从定义问题中出现的关键概念开始。例如，对于这个问题，它定义了素数是什么。

之后，思考过程就变得有意义了，并得出了优化的步骤。首先，它涵盖了基础知识：小于或等于 1 的数字不是质数，而 2 是唯一的偶质数。从那里，它检查数字是否可以被任何奇数整除，直到数字的平方根。这节省了时间，因为它避免了不必要的计算。此外，它不是测试每一个数字，而是跳过 2 以外的所有偶数，从而使过程更快。该函数用于Math.sqrt查找平方根，这限制了它需要检查的范围，使其保持高效和简单。 

再次，它还用小例子进行测试，就像上一个问题一样，比如已知的素数和非素数，以确保它按预期工作。

不过，还有一些改进的空间。例如，该函数不检查输入是否真的是数字，因此它可以更好地处理错误。它还可以包括以 0 或 5 结尾的数字的快捷方式，这些数字显然不是质数（5 本身除外）。我相信，添加一些关于为什么它跳过偶数或只检查平方根的解释也有助于初学者更好地理解它。

最后，我希望代码有一些示例使用测试，就像之前在测试中为我们提供 Python 代码的示例使用测试一样。

逻辑推理

现在让我们进行逻辑推理测试。

狼、山羊和卷心菜问题

我将测试一个经典的谜题：

“一个人要带着一只狼、一只山羊和一棵卷心菜过河。他的船只能载他自己和另一件东西。如果不去管它，狼会吃掉山羊，山羊会吃掉卷心菜。他怎样才能安全地把所有东西都运过河呢？”

我希望模型提供以下答案：

1. 开始： 一侧为人、狼、山羊、卷心菜
2. 男人带着山羊过河（狼和卷心菜一起安全）
3. 男子独自归来
4. 男子带狼过河
5. 男人把山羊带回来（狼和山羊不能单独相处）
6. 男子带着卷心菜过河
7. 男子独自归来
8. 男子牵着山羊过河
9. 结局：全部安全过关

但是让我们看看它如何处理思考过程，因为我不确定会发生什么！

为了便于阅读，我也需要截断此输出：

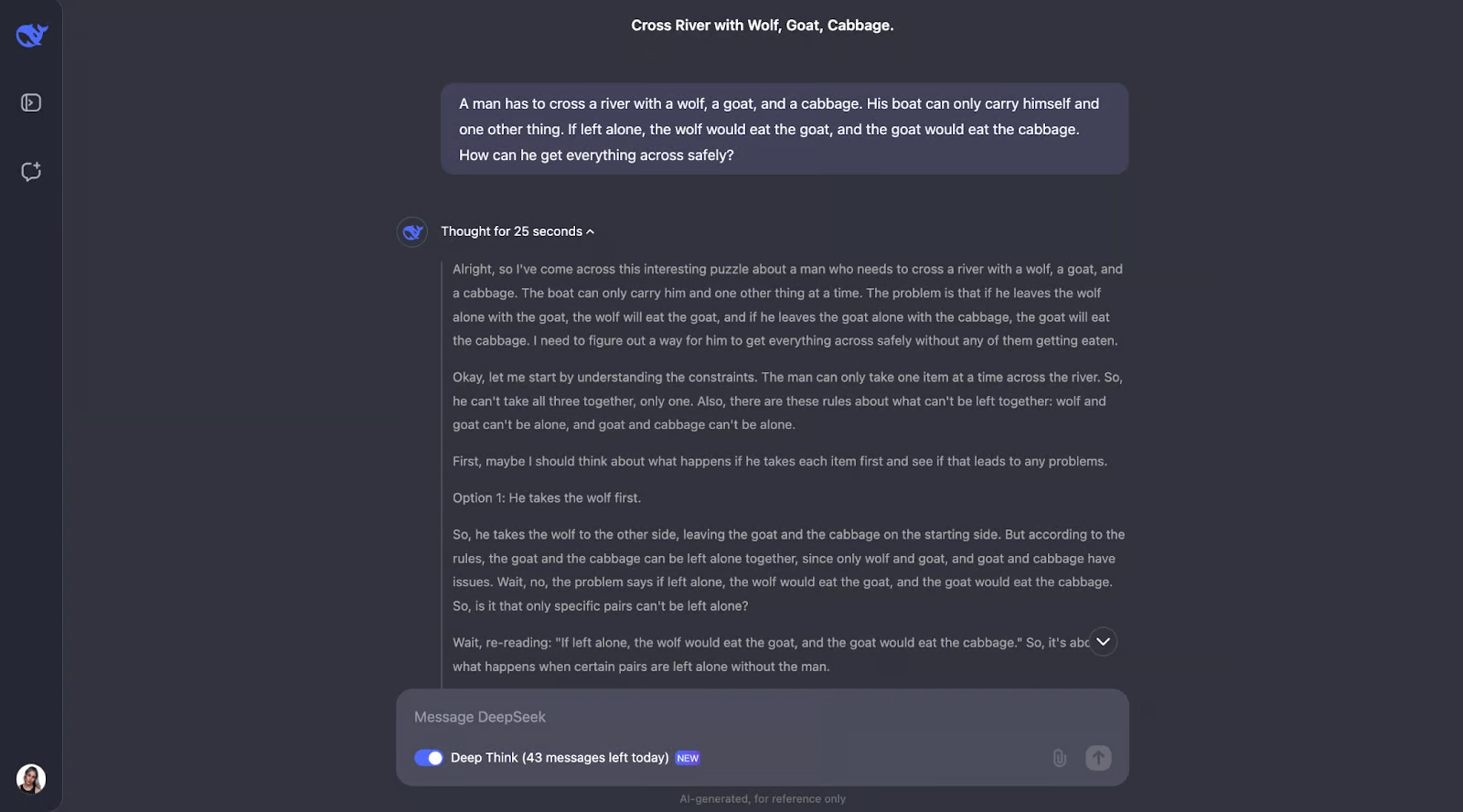
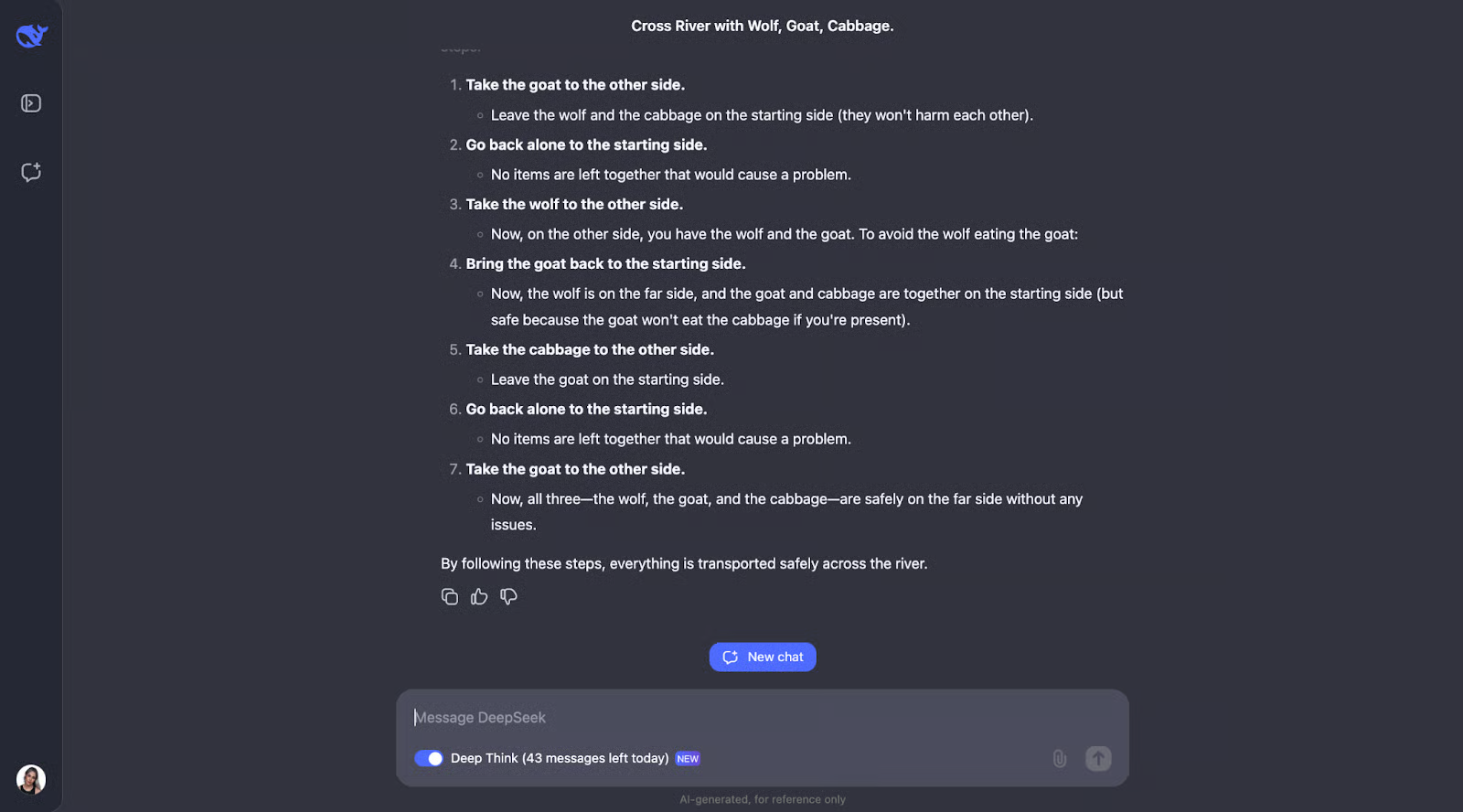
该模型在解决这个经典的过河难题方面做得非常出色。它仔细思考规则并检查不同的可能性。它知道有些组合，如狼和山羊或山羊和卷心菜，是不能单独存在的。它还会在开始时回顾约束条件。从这一点开始，它会考虑如果男人先带着每件物品过河会发生什么，并计算出这是否会产生任何问题。

我觉得非常棒的是，当某些事情行不通时，模型会调整计划。例如，当它先尝试选择狼，但意识到这会带来麻烦时，就会重新考虑步骤。这种反复试验的方法与我们人类自己解决难题的方式非常相似。

最后，模型得出正确的解决方案，并以清晰、逐步的方式进行解释。

称重球拼图

我们再试一次：

“你有 12 个球，外观完全相同。其中一个球比其他球重或轻。使用天平，找到奇怪的球，只需称重三次即可确定它是更重还是更轻。”

这个经典的逻辑谜题测试模型使用演绎推理得出最佳策略的能力。让我们看看会发生什么。这次的输出非常非常长，所以我需要直接跳到答案：

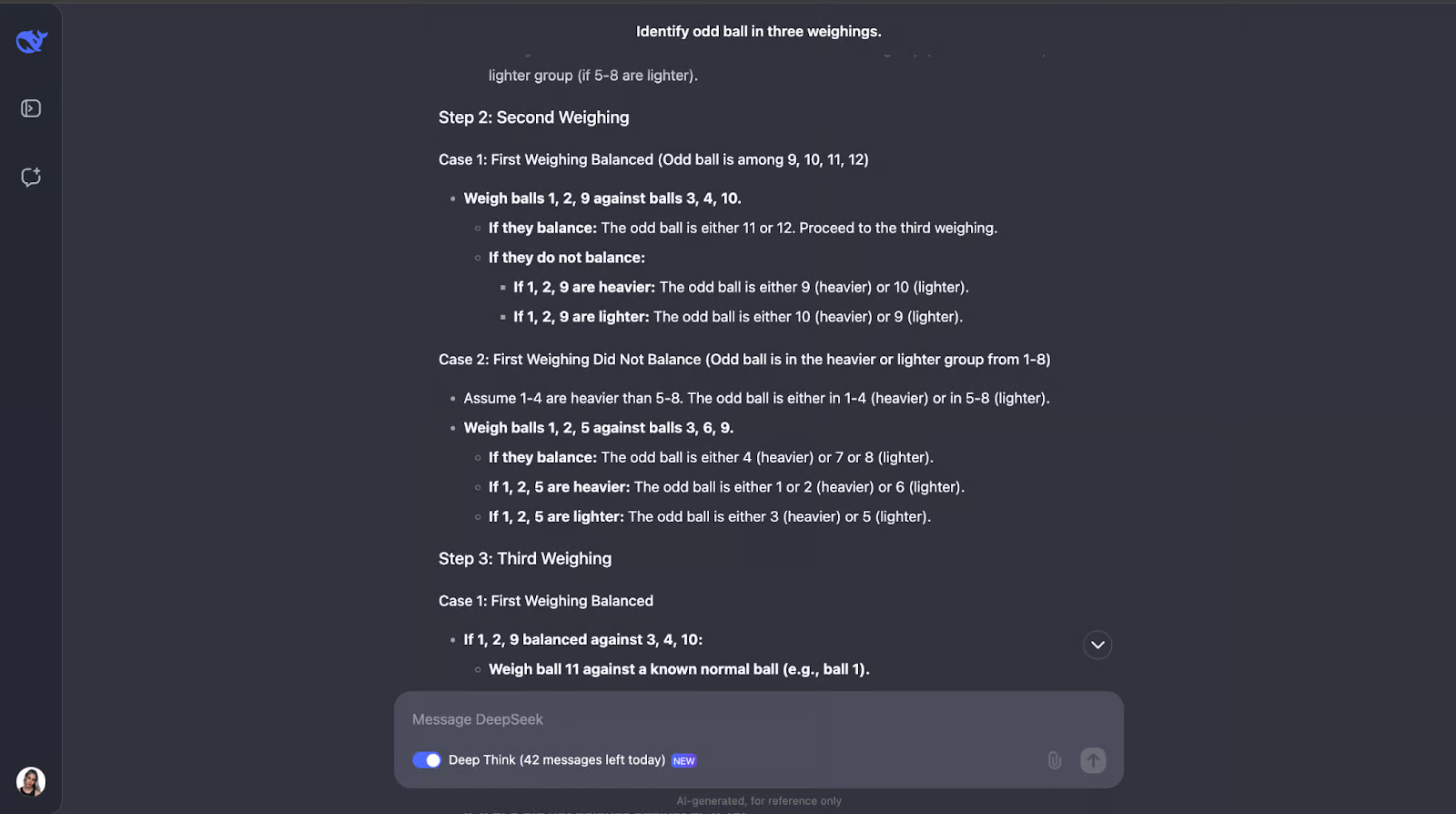
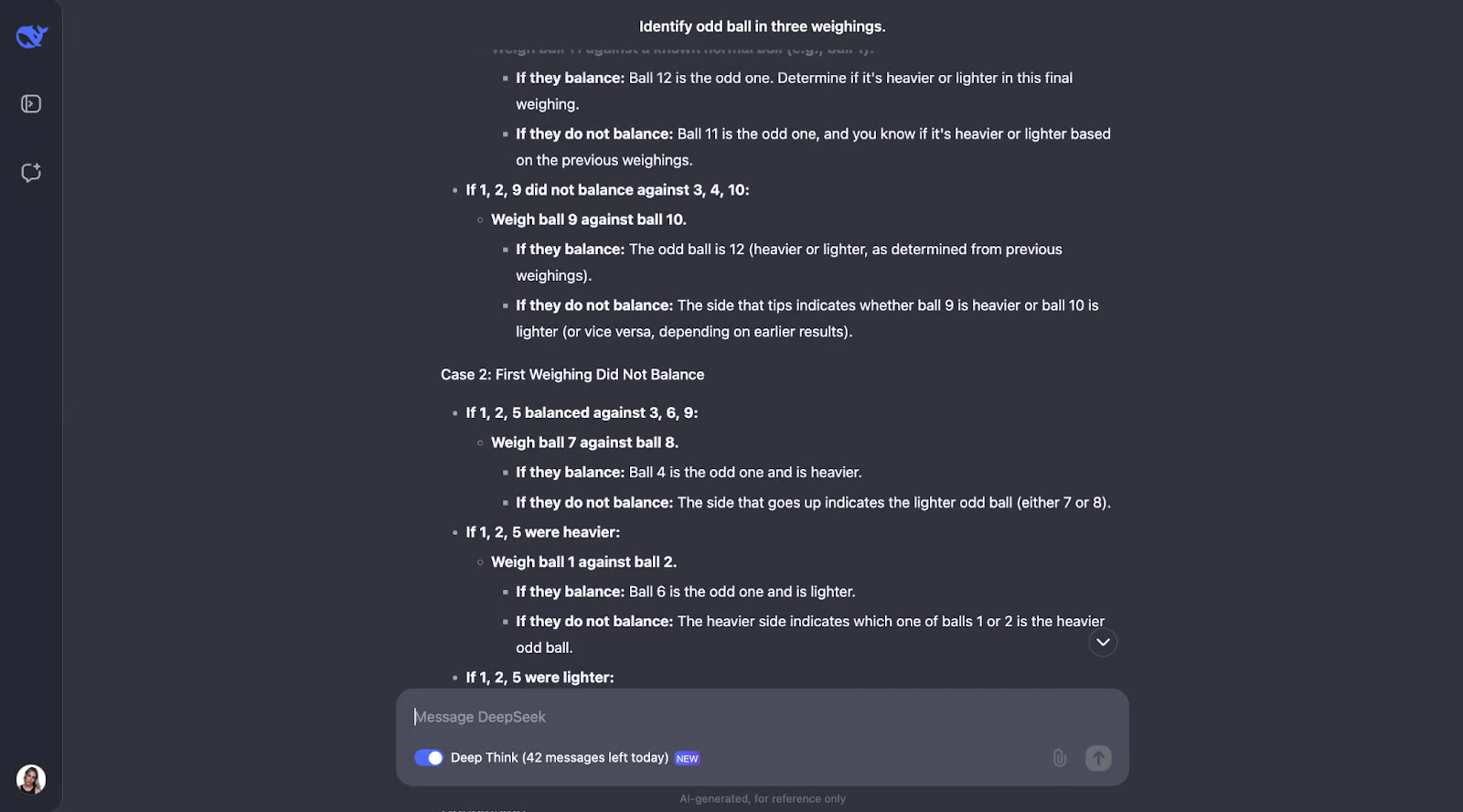
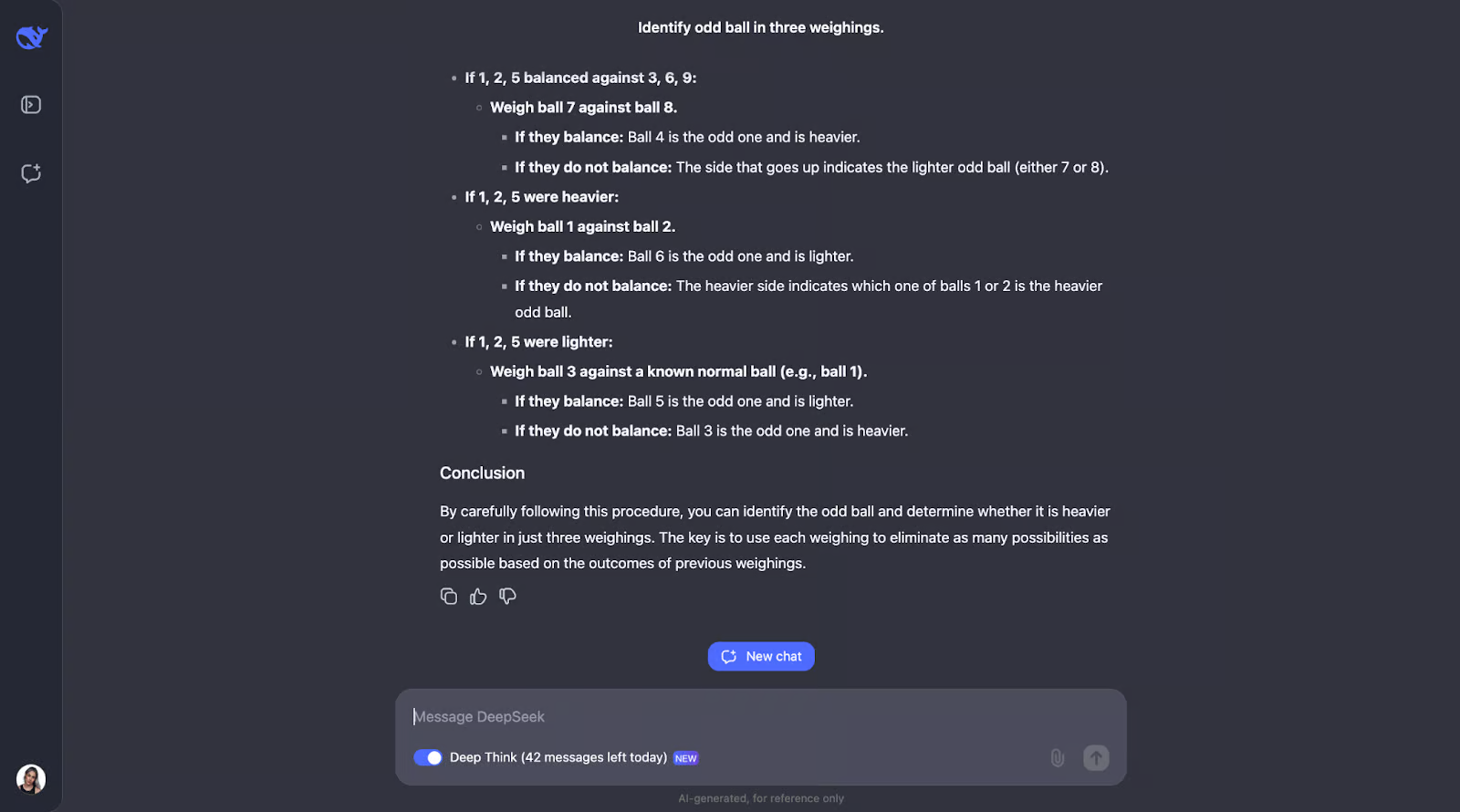
另一个我完全低估了输出长度的例子！模型意识到解决这个难题需要仔细规划，因为你只有三次机会。它还计算了结果和可能性的数量。

该模型的方法很聪明，因为每次称重都会排除尽可能多的可能性。它为所有结果（无论是秤重还是倾斜）做好计划，并根据发生的情况调整下一步。它非常详细，但步骤清晰、合乎逻辑，即使冗长，也很容易理解。

我非常喜欢的一点是，当方法开始变得有点过于复杂时，它会采用更系统或更简单的方法。不过，我认为对于像这样需要跟踪不同情况、结果和可能性的问题，添加图表或图表可能会帮助人们直观地了解思路并更好地理解输出。

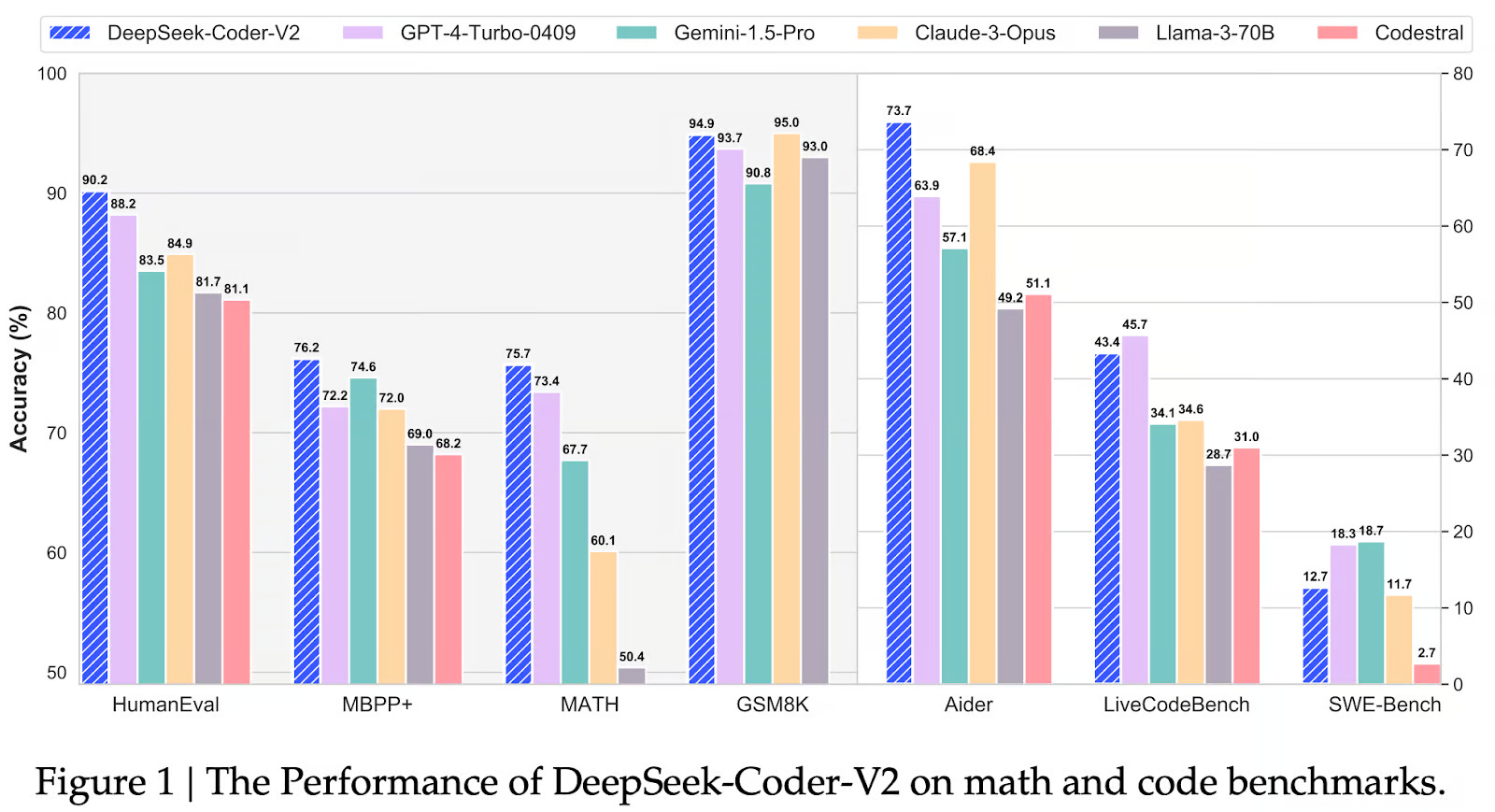
DeepSeek-R1-Lite-预览版基准

在本节中，我将在不同基准上比较 DeepSeek 与 o1-preview 和 GPT-4o 等其他模型的性能。每个模型都侧重于不同的技能，因此我们可以看到哪些模型在哪些方面表现最佳。让我们看看 DeepSeek 测量的基准：

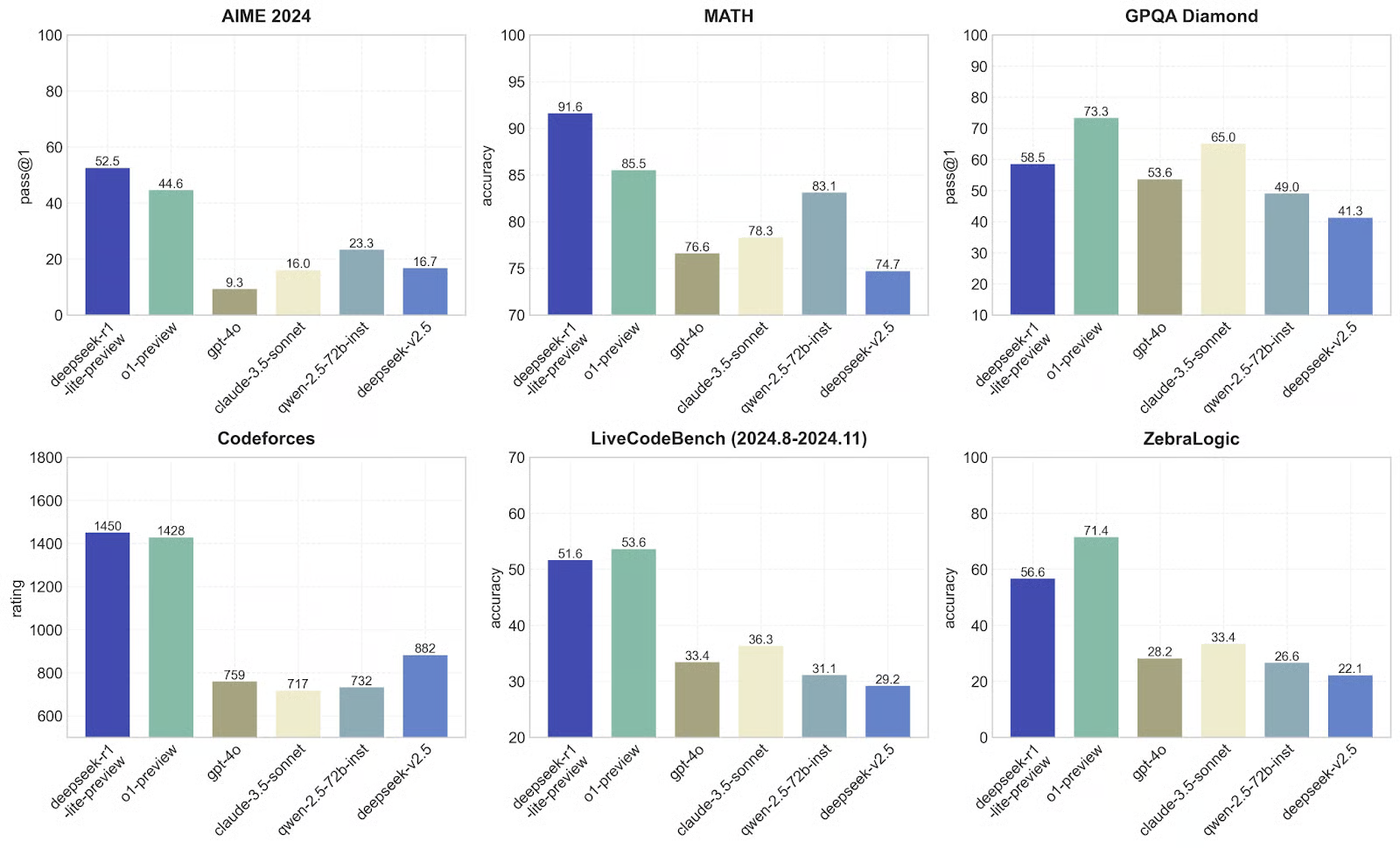
2024年国际医学博览会

DeepSeek-r1-lite-preview 显然是这里最好的，pass@1 为 52.5，其次是 o1-preview，为 44.6。其他模型，如 GPT-4o 和 claude-3.5-sonnet，表现要差得多，得分低于 23。这表明 DeepSeek-r1-lite-preview 模型在处理 AIME 基准测试特有的高级数学或逻辑问题方面相当出色，在我进行测试后，我对此并不感到惊讶。

数学

DeepSeek-v1 再次以惊人的 91.6 准确率占据主导地位，远远领先于 o1-preview（85.5），并且比 GPT-4o 等其他模型好得多，后者很难达到 76.6。这表明 DeepSeek 擅长解决数学问题，这证实了我从之前进行的测试中的经验证据得出的假设——到目前为止没有意外！

GPQA 钻石

在这里，o1-preview 的表现优于 DeepSeek-v1，其 pass@1 为 73.3，而 DeepSeek-v1 为 58.5。其他模型（如 GPT-4o）则落后于 53.6。这表明 o1-preview 更适合涉及回答问题或基于逻辑推理解决问题的任务。DeepSeek 仍然表现稳健，但不如 o1-preview 好。

代码力量

对于竞技编程，DeepSeek-v1（1450）和 01-preview（1428）几乎并列第一，而其他模型如 GPT-4o 的得分仅为 759 左右。正如预期的那样，这表明这两个模型在理解和生成编程挑战的代码方面非常出色。

活码测试

这会测试一段时间内的编码能力，o1-preview 略胜 DeepSeek-v1（53.6 vs. 51.6）。其他模型（如 GPT-4o）则落后很多，得分为 33.4。这再次表明 DeepSeek 和 01-preview 都非常适合编码，但 01-preview 在这些任务上表现更好一些。

斑马逻辑

o1-preview 在这方面领先，准确率为 71.4，而 DeepSeek-v1 的准确率为 56.6。其他模型的表现要差得多。这表明 o1-preview 更擅长处理 ZebraLogic 等抽象逻辑任务，这些任务需要更多的创造性或跳出框框的思维，这与我从测试中获得的结果一致，因为创造力绝对不是 DeepSeek-v1 的强项。

这些图表证实了 DeepSeek-v1 在数学和编程挑战方面的表现非常出色。我想说 o1-preview 更加平衡，在更广泛的任务中表现良好，这使其更加通用。

现在让我们看一下这张图表：

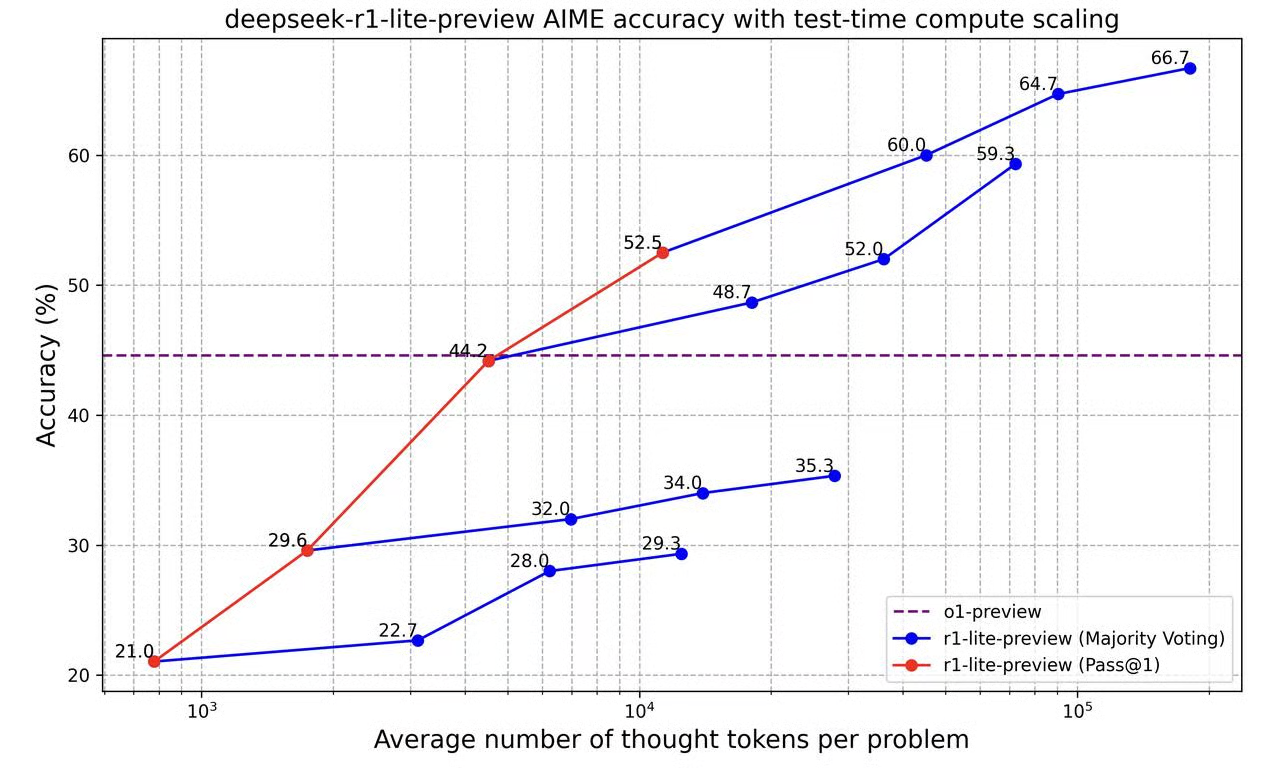
此图显示了“deepseek-r1-lite-preview”模型在处理更多信息时解决问题的能力如何提高（以其使用的“思想标记”数量衡量）。它比较了两种衡量模型准确度的方法：

1. Pass@1（红线）：这是模型给出第一个答案时的准确率。随着使用更多标记，其准确率从 21% 提高到 52.5%。这意味着模型在有更多时间思考时会做得更好，即使只是第一次回答。
2. 多数投票（蓝线）：在此，模型会给出多个答案，并选出它最常建议的答案（多数投票）。这种方法的准确率从 22.7% 开始，随着使用的标记越来越多，准确率会提高到 66.7%。它总是比第一个答案的方法更准确，这表明让模型多次尝试有助于它做出更好的决策。

紫色虚线表示准确率稳定的 o1-preview 模型。一开始，o1-preview 更好，但随着 DeepSeek r1-lite-preview 可以使用更多思维标记，它超越了 o1-preview，变得更加准确。

所以基本上，这张图表表明，让 DeepSeek r1-lite-preview 多思考并多次尝试可以提高其准确性。

结论

DeepSeek-r1-lite-preview 比 OpenAI 的 o1-preview 好吗？嗯，这取决于任务。对于数学和编码问题，我认为是的。对于逻辑推理，这取决于任务。 

真正让我吃惊的是它如何推理一些测试。它确实让我思考模型“思考”的真正含义以及它是如何得出推理方法的。

如果你对这个模型很好奇，为什么不自己测试一下呢？在你感兴趣的任务上试用一下，看看它的表现如何——你可能会像我一样感到惊讶！